ニュートンの記法(にゅーとんのきほう、英 Newton's notation )は、数学における微分の記法のひとつである。 この記法は アイザック・ニュートン が fluxion ( 流率・流動率 ) 1 と呼称した 時間 に対する変化率を表すために導入したもので、 関数 名の上部に 微分 の階数と同数の ドット符号 を記About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creatorsニュートン法 例26 baileysce ベイリー法 例27 newton_2dsce 2変数のニュートン法 第 3 章 代数方程式の数値解法 Scilab プログラム 備考 例31 algebraic_newtonsce ニュートン法 例32 bairstowsce ベアストウ法 第 4 章 連立 1 次方程式の数値解法 - 消去法 Scilab

ニュートン法による逆数の計算 Dinop Com
微分 ニュートン法
微分 ニュートン法-2 ニュートンの運動方程式 8 そして、L をx とx_ で微分する。 @L @x = dV dx @L @x_ = mx_ ∴ d dt (@L @x_) = m x よって、ニュートンの運動方程式から次の式が導かれる。 d dt (@L @x_) @L @x = 0 この式を、ラグランジュの方程式という。これは、ニュートンの運動方程式と 非正則な複素関数のニュートン法 複素関数 f(z) が非正則(複素微分できない)場合というのは,実は世の中に多くある. たとえば, f(z) = z 2 は複素微分できないので非正則関数である. しかし, f(z) の実部と虚部がそれぞれ z = x iy の x や y で微分




ニュートン法とは 定義と性質 理数アラカルト
ニュートン・ラプソン法で確認しましょう。 関数の微分(導関数)は f'(x) = 2x です。 図7多次元ニュートン法 野下浩司 多次元ニュートン法を用いて,被食捕食系の平衡点を見つけることを目指す.ここで は出来るだけ簡単な方法でプログラムを書こう. 1 解きたい問題 被食捕食系 8 >>> >>< >>> >> dx dt = ax bxy (1) dy dt = cxy dy (2) 準ニュートン法では目的関数の1階微分までしか使わない。そのなかでもbfgs公式による準ニュートン法では反復ごとに最大 \(n^2\) の計算で済む。 bfgs公式による準ニュートン法 準ニュートン法ではヘッセ行列を逐次計算によって近似したものをつかう。
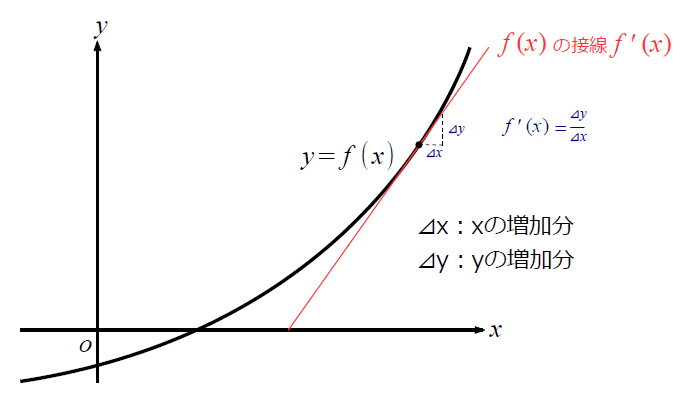
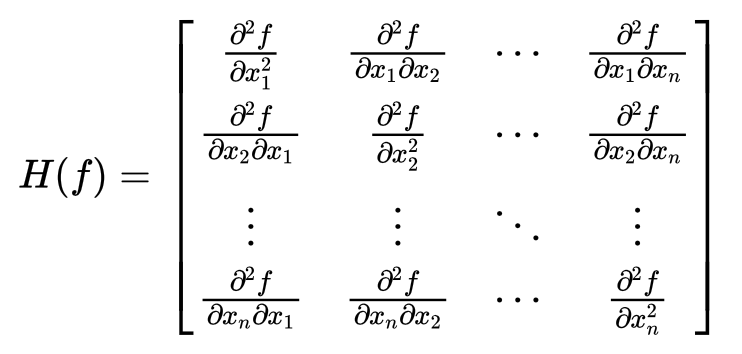
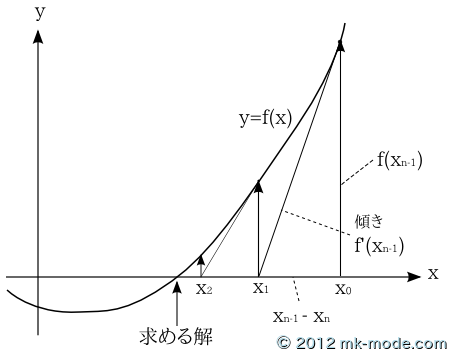
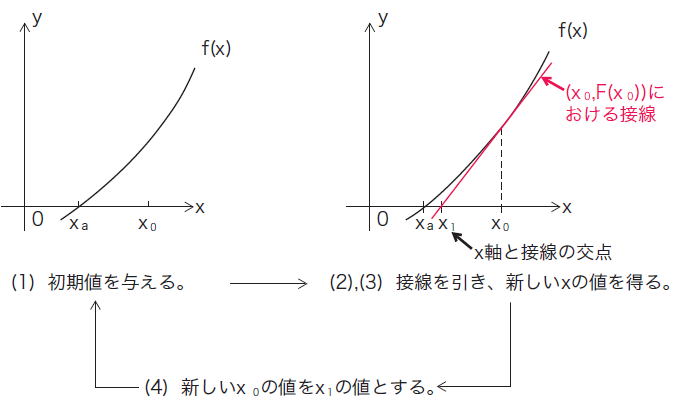
ニュートン法の問題点 初期点x = 1/2 のとき ⇒ヘッセ行列はHf(x) = 5(正定値でない) ⇒ニュートン方向に進むと関数値が増加する ヘッセ行列が正定値でない場合には 目的関数値が増加する可能性あり4321 0 1 22 15 1 05 0 05 1 15 2 f を2次近似する と上にニュートン法 連続で1 回微分可能な関数y=f(x) を考える。 ある点xn での導関数f'(xn) が与えられるとき、(xn,f(xn)) を通り、傾きがf'(xn)の直線方程式は ニュートン法 、または ニュートン・ラフソン法 は、数値解析の分野いおいて、方程式を数値計算によって解くための反復法による球根アルゴリズムの一つです。 手順としては、関数 f ( x) f (x) f (x) について、 ある x 1 x_1 x1 の数値を決定する
ニュートン法 を使って適当な初期値の元に解け。 微分方程式とルンゲクッタ法 常微分方程式 を解析的解くには となり、境界条件を入れて解けば となる。これは解析解であるがルンゲ・クッタ法を使った数値解は次のように補間関数の形で求まる。 問題ニュートン法 x の関数 f(x) について,f(x) = 0 を満たす解を求める方法をニュートン法という. R では関数 uniroot() でニュートン法が行える.以下では 0 ≦ x ≦ 2 の範囲において,f(x) = x 3 2 が 0 となる x の値を求めている.Newton方程式は2階の常微分方程式です。 したがって1階の常微分方程式であるオイラー法 (STEP04 で学んだ)を直接用いて解くことはできません。 オイラー法を用いて解くためには、まず2階の微分方程式を1階の連立微分方程式に書き直してやる必要があります。



Newton法
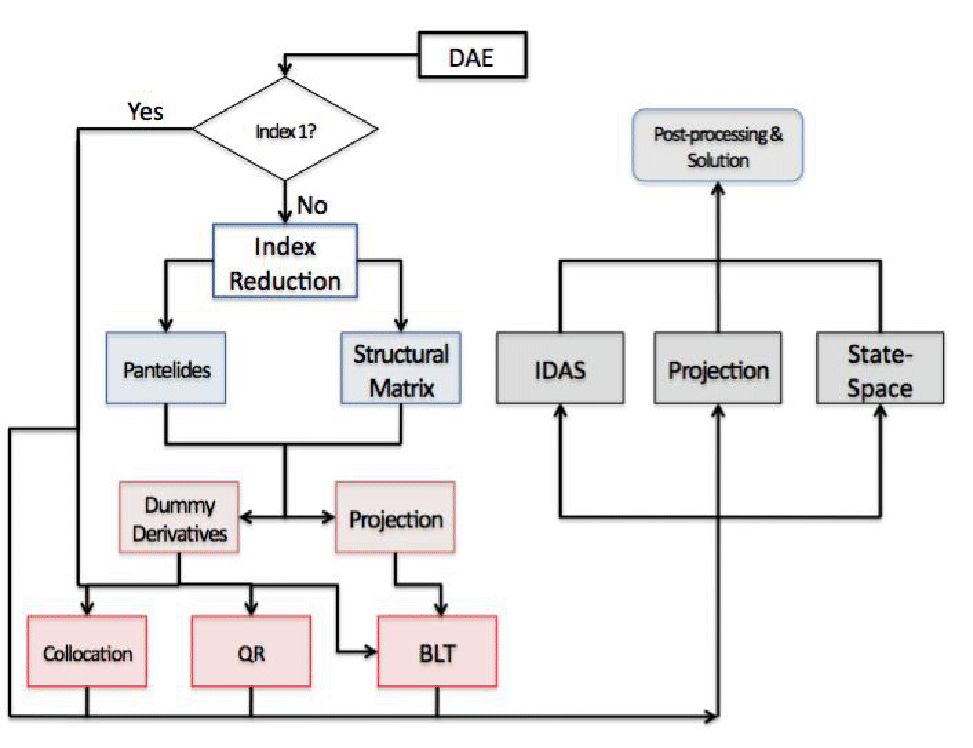



微分代数方程式の数値解法 Wolfram言語ドキュメント
入試問題の背景としてのニュートン法 レベル ★ 最難関大受験対策 極限,微分 更新日時 ニュートン法 は,コンピュータを用いて方程式の解を高速に計算する手法です。 ニュートン法と呼ばれる手法に関連した入試問題とその背景を解説します アイザック・ニュートンによるニュートンの記法は微分のドット記法とも呼ばれ、従属変数の上部にドット記号「・」を記して =, =, などのように表す。しばしば速度や加速度のような時間微分の表現法として使用される。 少し前には、\(f(x)=0\) の解を2分法により求める C アルゴリズムについて紹介しました。 C 非線形方程式の解法(2分法)!今日は、方程式 \(f(x)=0\) の解をニュートン法により求める C アルゴリズム についてです。ニュートン法の概念・アルゴリズムは以下の通り。
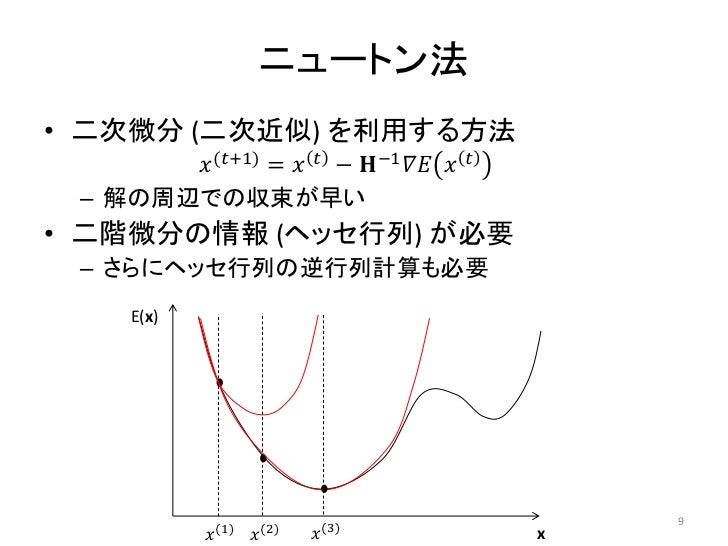



Cvim 11 3 最小化のための数値計算



ニュートン ラフソン法 Pukiwiki For Pbcg Lab
これを数式であらわすと微分方程式になるわけです。 2 非斉次の1階微分方程式の解法 21 ニュートンの冷却の法則 熱したお湯の時刻tでの温度をu(t)とおく この温度は室内温度T0 とするとき, その差に比例して冷却すると言う(ニュートンの冷却の法 則)を微分可能な関数とするとき,ニュートン法は各 反復において, 次の線形化された方程式を解くこと により点列fxkg を生成する. F(xk)F0(xk)(xk1 ¡xk) = 0 (1) このニュートン法について,以下のような収束定 理が成り立つ6. 定理11 Fニュートンの記法 (にゅーとんのきほう、 英 Newton's notation )は、 数学 における 微分の記法 のひとつである。




ニュートン法 ニュートン ラフソン法 明治大学 理工学部 応用化学科 データ化学工学研究室 金子 弘昌 Ppt Download
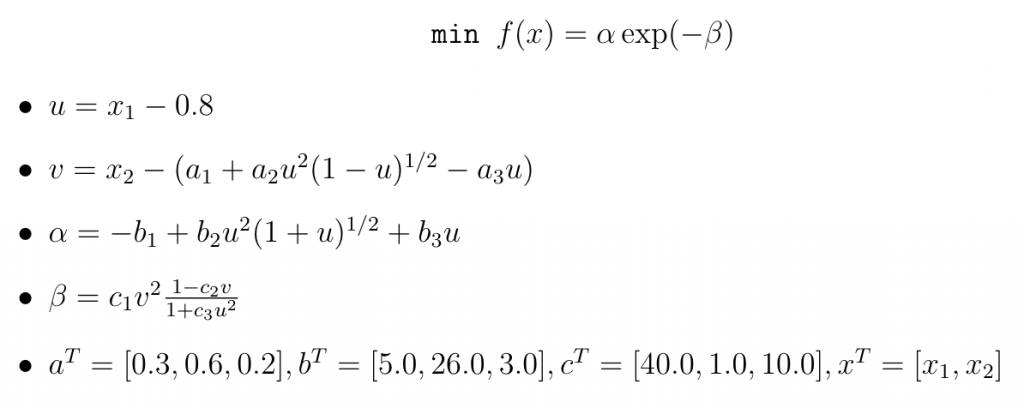



ニュートン法 Miidas Research
ニュートンラフソン法 ニュートンラフソン法 目次へ NewtonRaphson法 二分法は,二つの仮定値の間に一つの解が存在する場合,確実に解を得ることができる. 近似解を得るための収束判定誤差を小さくすることで,高精度の結果を得ることができ 第68回 微分・積分の数学 ニュートン・ラフソン法 後編 09年10月8日 平田敦 数学, Java, 微分, 積分, ニュートン・ラフソン法ニュートン法 二分法では、 を半分ずつにすることで探索の効率を高めました。 より効率を高める方法はあるでしょうか? が の平方根であるということを、 が以下の方程式の解であると言い換えることにしましょう。 この方程式の近似解が高速に求まれば平方根が得られそうです。




遂次近似法2 ニュートン法 理論 身勝手な主張
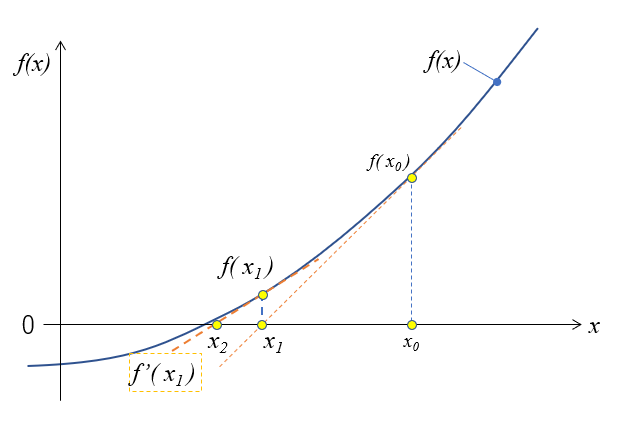



平方根を数値計算で求める ニュートン法 仕事と投資とあと何か
ガウス・ニュートン法とレーベンバーグ・マーカート法 ほげ 21年2月7日 1 ニュートン法 ニュートン法は, 2 階微分可能な関数f(x) を, x に関して最小化するための逐次的な手法である6 その派 生であるガウス・ニュートン法や, レーベンバーグ・マーカート法は, グラフベースSLAM の基礎となるポーも同様で,微分法の性質(積の微分と合成関数の 微分)だけを使っており,具体的に微分を実行し ているわけではないからである。 そういう事情から,『力学i』では,力学と微分積 分を平行して導入することを主たる目標とし,「変微分法の誕生(ニュートンの流率法) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're




ニュートン法による逆数の計算 Dinop Com
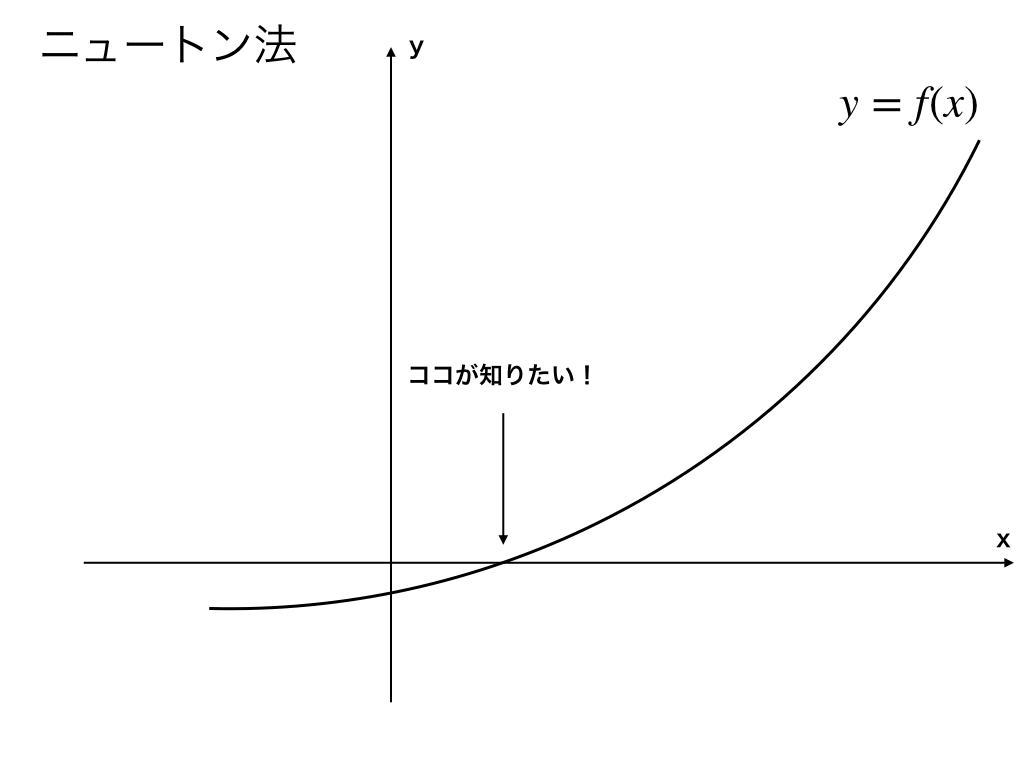



ニュートン法の仕組みと証明の仕方を分かりやすく解説
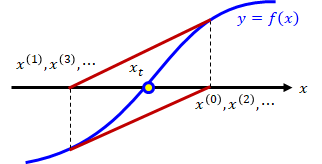
Newton 法とは, 次の図を根拠に近似解を計算する方法です 函数 が微分可能かつ下に凸であるとき, の解 を次の方法で求めます まず, に近い値 を 1つとり, 関数 のグラフ上の点 における接線が, 軸と交わる点の 座標 を としますニュートン記法の微分記号 微分記号の記法としては といったライプニッツの記法が一般的です。 しかし力学系等の分野によっては のようなニュートンの記法の方が好まれる場合もあります。 文字の右側にカーソルを位置付け右クリック、「プロパティニュートンの議論を次の二つのステップで示す: 1 F(x) = kxs, s = m n とするとF′(x) = ksxs−1 2曲線の下の部分の面積を とすると ニュートンの微積分法– p2/15




ニュートン法 数値計算 Youtube



ニュートン法とは 制御工学の基礎あれこれ



Newton法
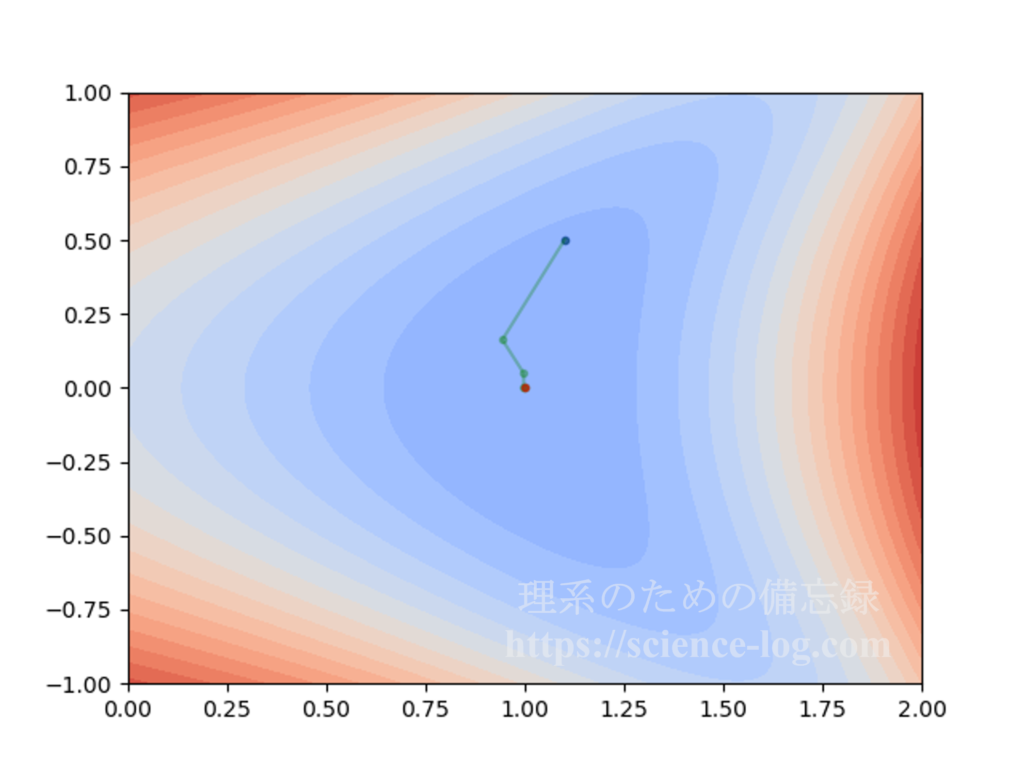



最適化問題の基礎 ニュートン法とヘッセ行列 理系のための備忘録



最急降下法とニュートン法を用いた最適化 Qiita



Newton法




Cvim 11 3 最小化のための数値計算




ニュートン法で方程式の近似解を求める 薬剤師のプログラミング学習日記



Newton法 Pythonで数値計算プログラムを書き直そうシリーズ Qiita
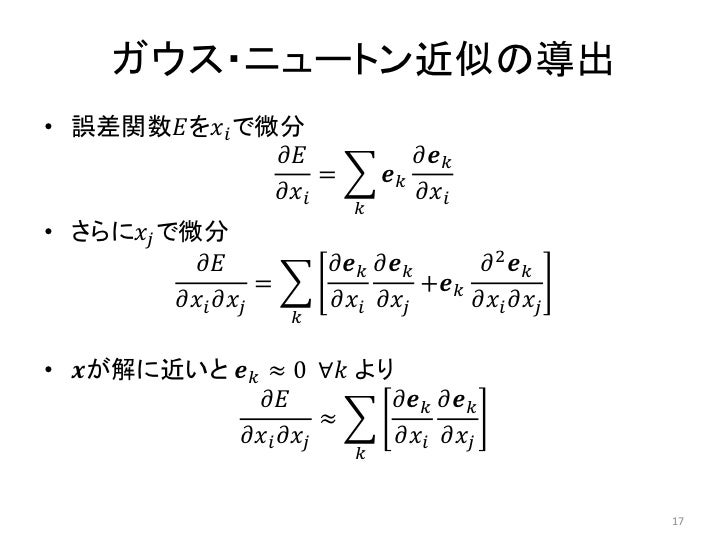



Cvim 11 3 最小化のための数値計算
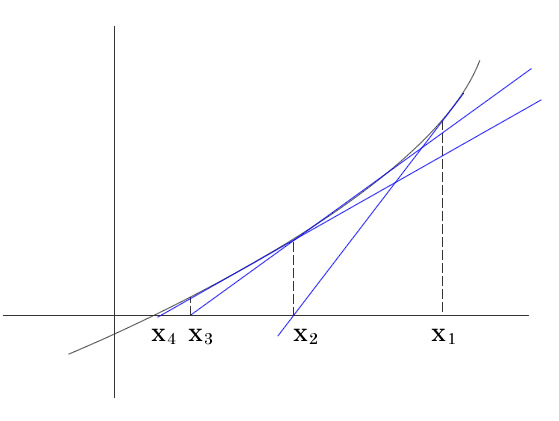



ニュートン法で近似解 Python Numpy 優技録



セカント法による求根 Thoth Children



技術計算製作所 ニュートン法 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Numcal Newton




ニュートン法 Youtube



ニュートン法とは 制御工学の基礎あれこれ




Amazon Co Jp 確率微分方程式に対するnewton法 発見的なアルゴリズムの定式化から確率論的二次収束まで Ebook 天野一男 Kindleストア



数値微分 ゆるゆるプログラミング



逆数の計算を計算の置換えで早くする Thoth Children
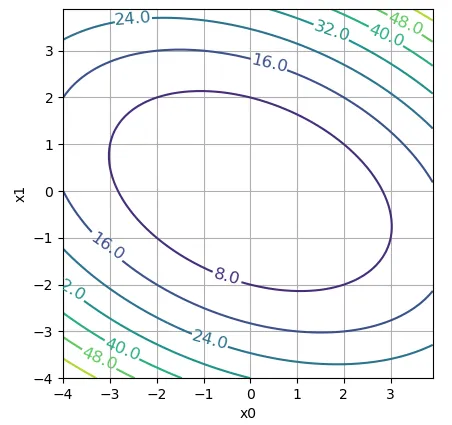



準ニュートン法による最適化とpythonによる実装 Helve Tech Blog



ニュートン ラフソン法



Broyden法による求根 Thoth Children




最適化問題の基礎 ニュートン法とヘッセ行列 理系のための備忘録



数値解析入門 Newton法
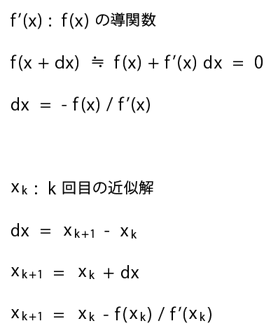



37 Newton 法 1 2 Shade Labo 開発フォーラム Shade3d フォーラム



ニュートン法とは何か ニュートン法で解く方程式の近似解 Qiita




Cプログラミング演習 ニュートン法による方程式の求解 Ppt Download




ニュートン法 前提と考え方 Youtube



ニュートン法 Miidas Research




一言で言えばbfgs 準ニュートン法の紹介



数値解析入門 Newton法




ニュートン法によってルート 円周率の近似値を求めてみよう 趣味の大学数学



C 非線形方程式の解法 ニュートン法 Mk Mode Blog




非線型方程式の解法 ニュートン法のアルゴリズム Youtube
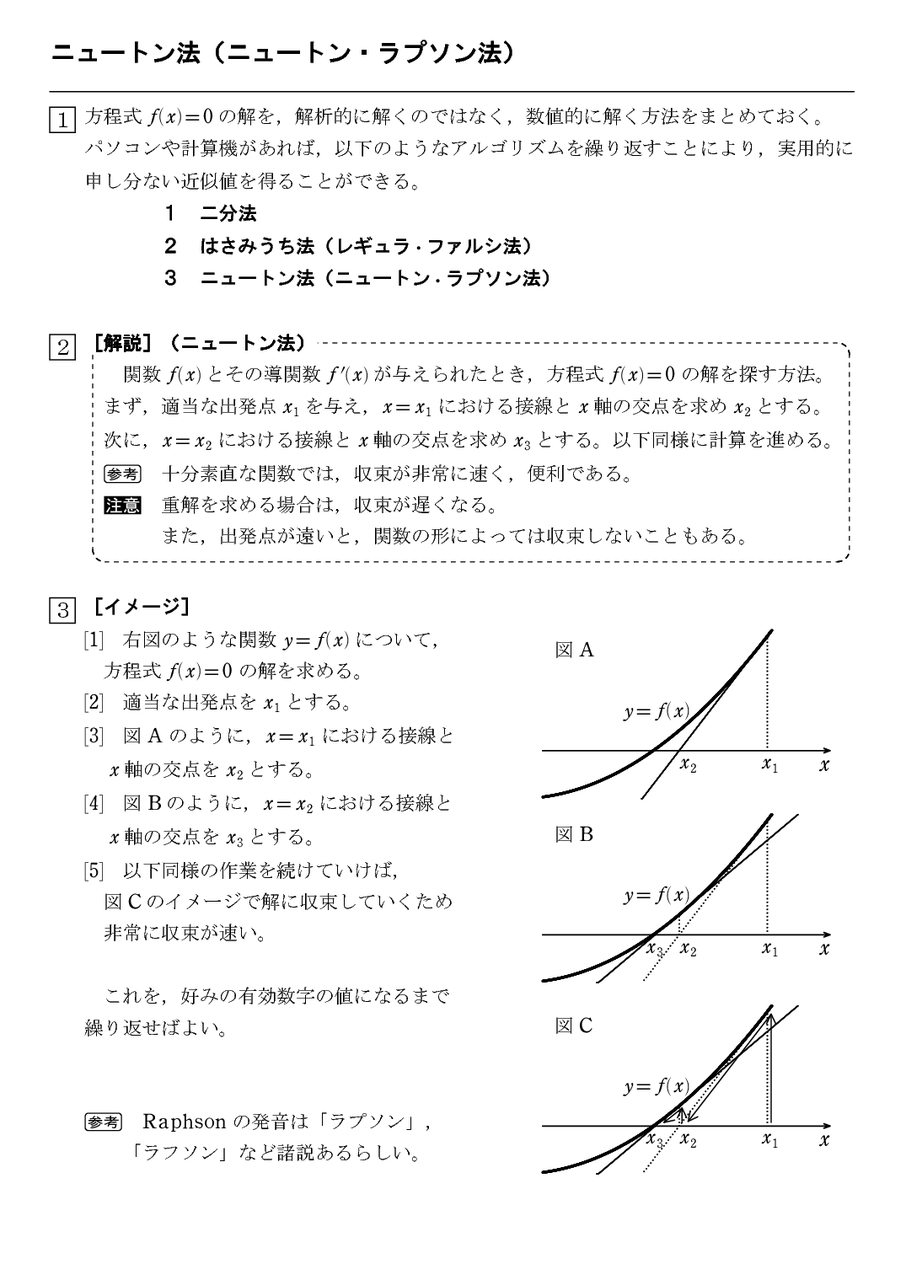



ニュートン法 ニュートン ラプソン法 1 怜悧玲瓏 高校数学を天空から俯瞰する



2 非線型方程式




ニュートン法とは サイエンスの人気 最新記事を集めました はてな
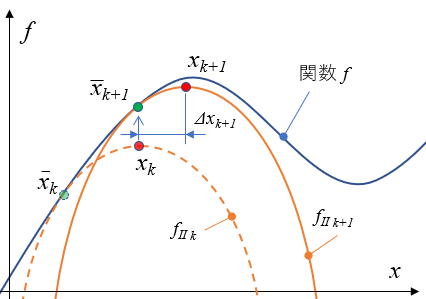



ニュートン法はどのように収束していくのか 1変数の場合で視覚化 仕事と投資とあと何か
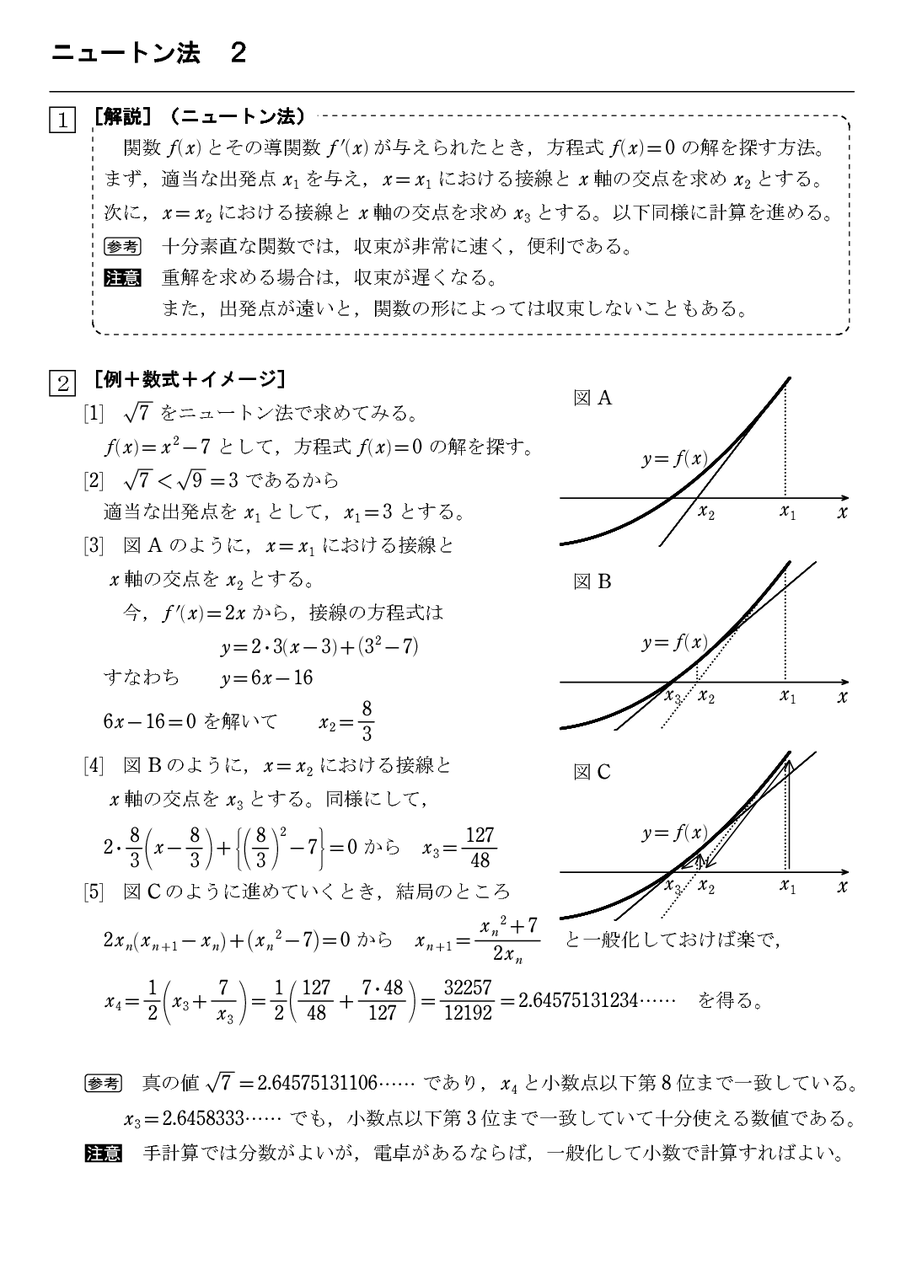



ニュートン法 ニュートン ラプソン法 2 怜悧玲瓏 高校数学を天空から俯瞰する



ニュートン法とは 制御工学の基礎あれこれ
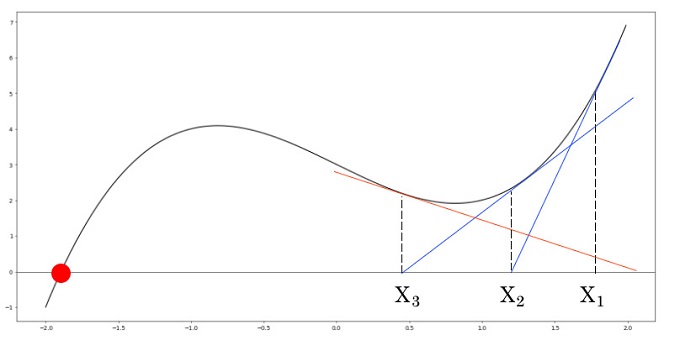



ニュートン法で近似解 Python Numpy 優技録



1




ニュートン法 Wikipedia




ニュートン式 超図解 最強に面白い 微分積分 Amazon Com Books
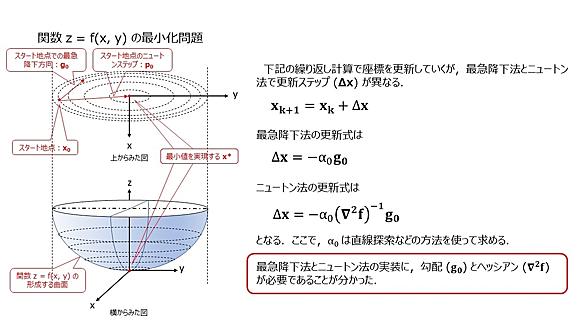



ニュートン法とは サイエンスの人気 最新記事を集めました はてな
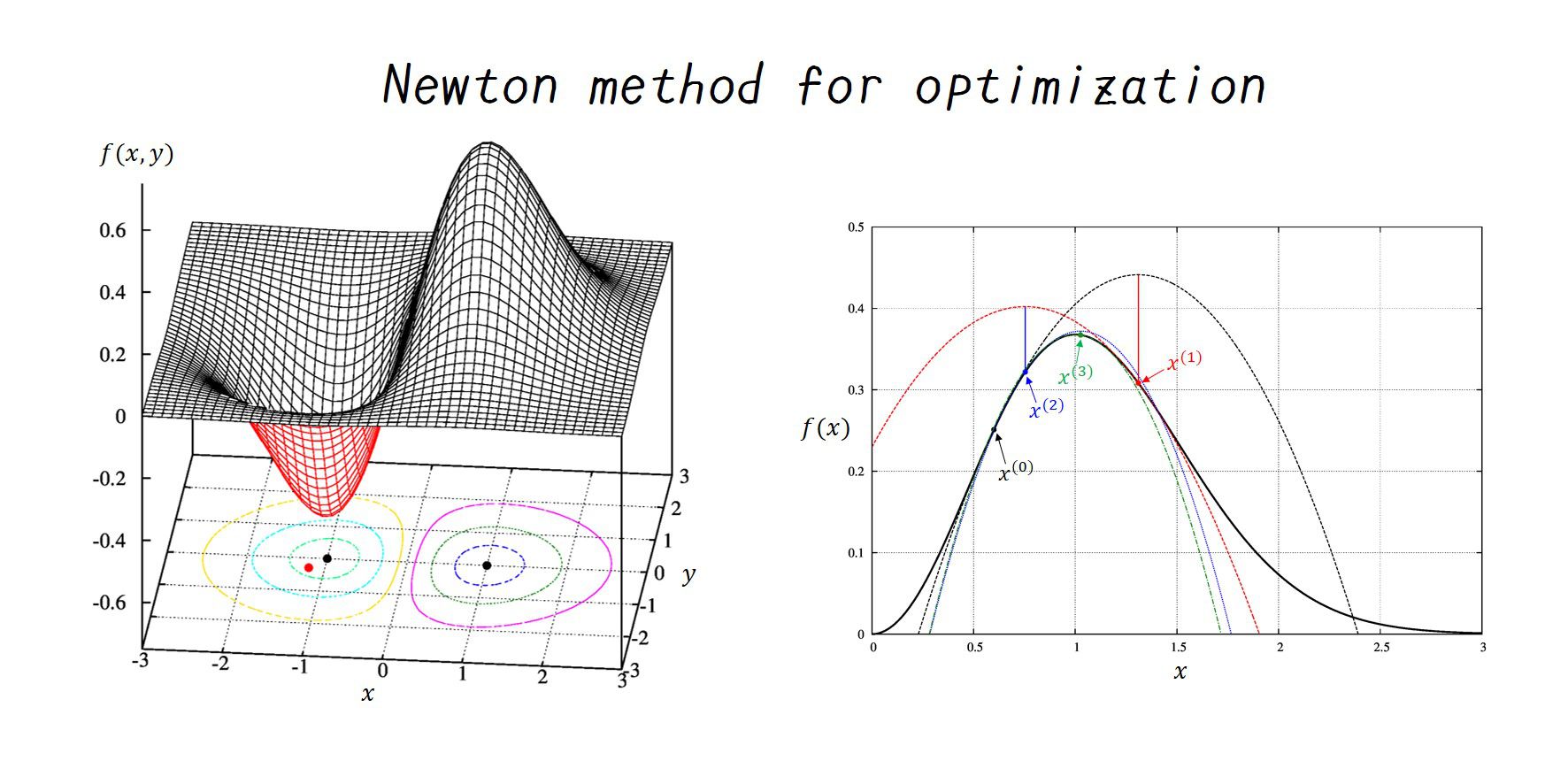



極値を求めるニュートン法 シキノート
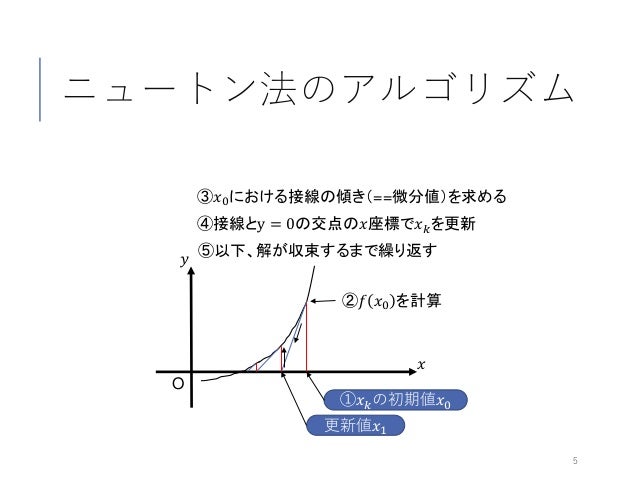



Vbaで数値計算 04 ニュートン法
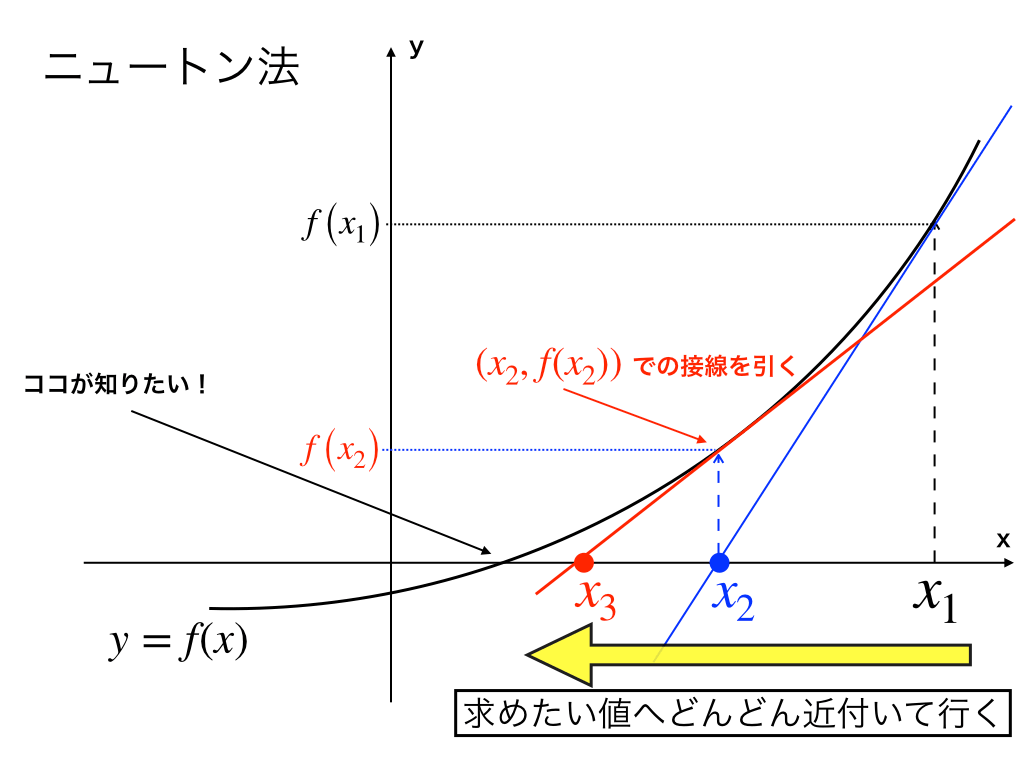



ニュートン法の仕組みと証明の仕方を分かりやすく解説
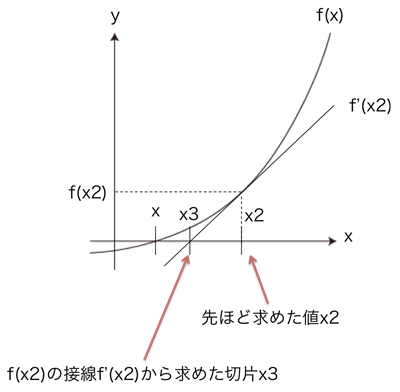



ニュートン法とは何か ニュートン法で解く方程式の近似解 Qiita




一言で言えばbfgs 準ニュートン法の紹介




書記が数学やるだけ 16 ニュートン法による近似 最適化のアルゴリズム 21 01 17追記 鈴華書記 Note
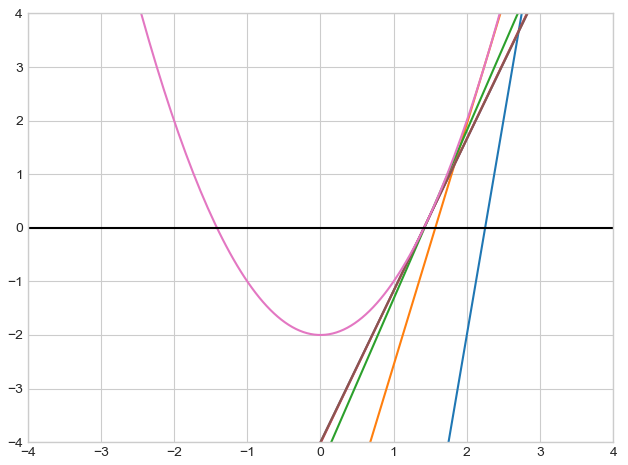



ニュートン法 Miidas Research




制約条件のない最適化 非線形方程式の解法 Wolfram言語ドキュメント




Pythonで方程式を解く方法 Scipy ニュートン法 二分法による計算 Monte Carlo Note



Kj4




Cvim 11 3 最小化のための数値計算




ニュートン法とは 定義と性質 理数アラカルト
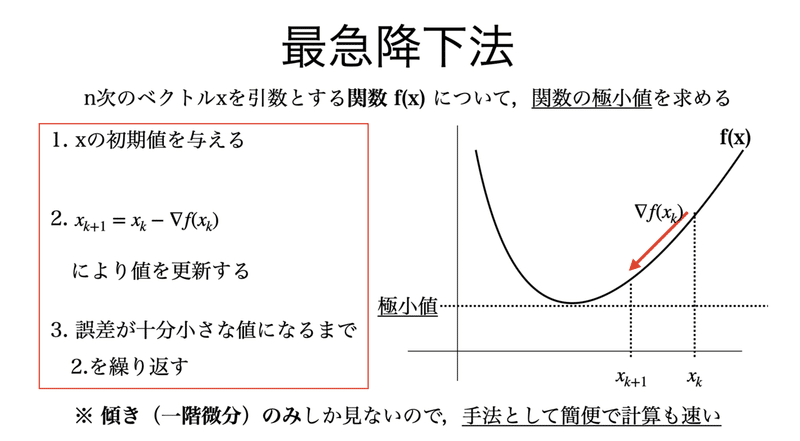



書記が数学やるだけ 16 ニュートン法による近似 最適化のアルゴリズム 21 01 17追記 鈴華書記 Note




Newton別冊 微分と積分 新装版 ニュートン別冊 本 通販 Amazon
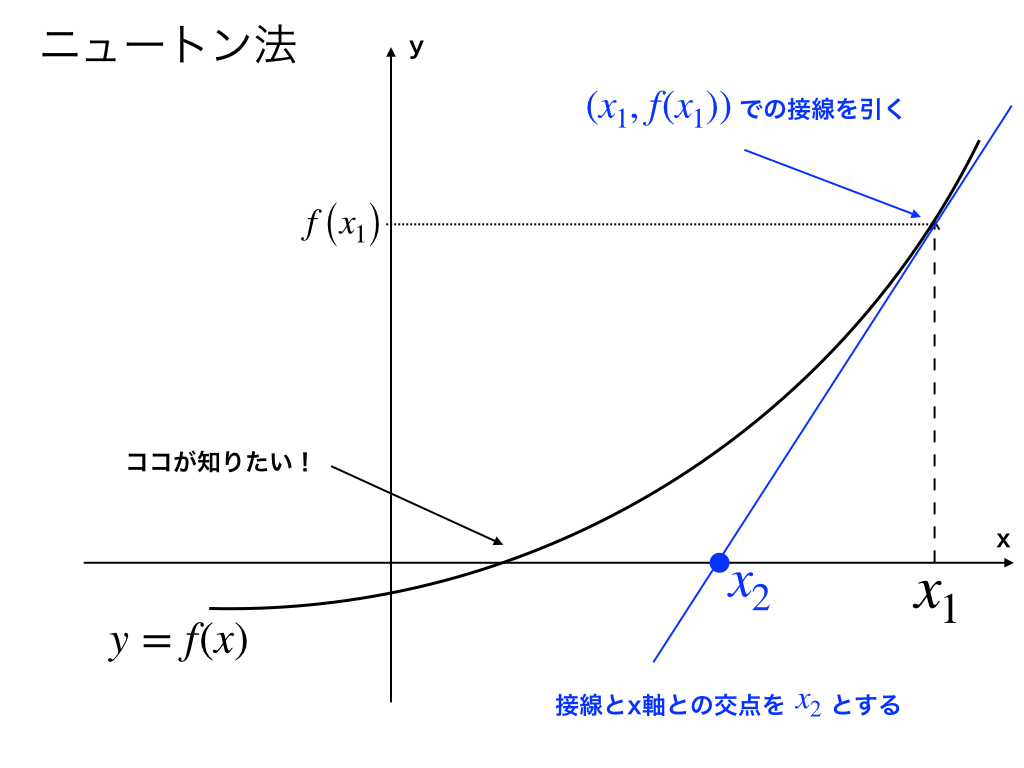



ニュートン法の仕組みと証明の仕方を分かりやすく解説




Cvim 11 3 最小化のための数値計算




Cvim 11 3 最小化のための数値計算
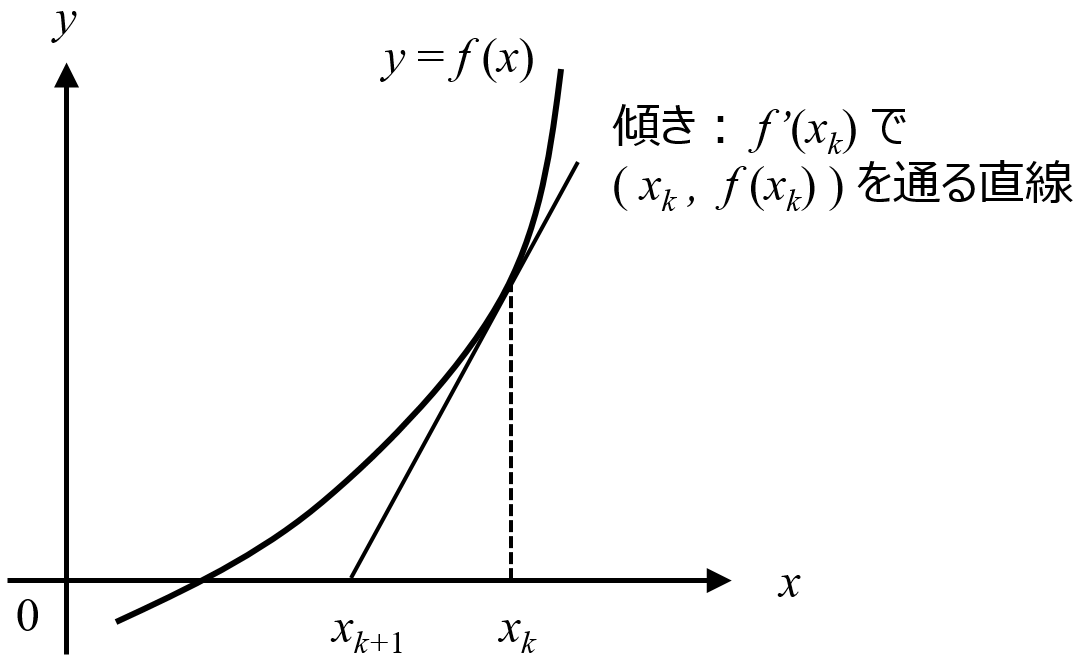



ニュートン法 ニュートン ラフソン法 F X 0の解を数値的に求める



第67回 微分 積分の数学 ニュートン ラフソン法 前編 はじめmath Javaでコンピュータ数学 Gihyo Jp 技術評論社




C言語 ニュートン法のプログラムの為の数値微分 Visual Studioでc C言語 C C 教えて Goo
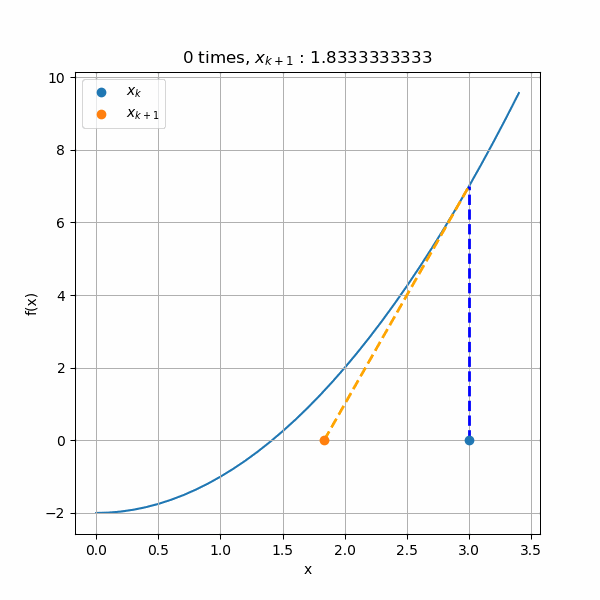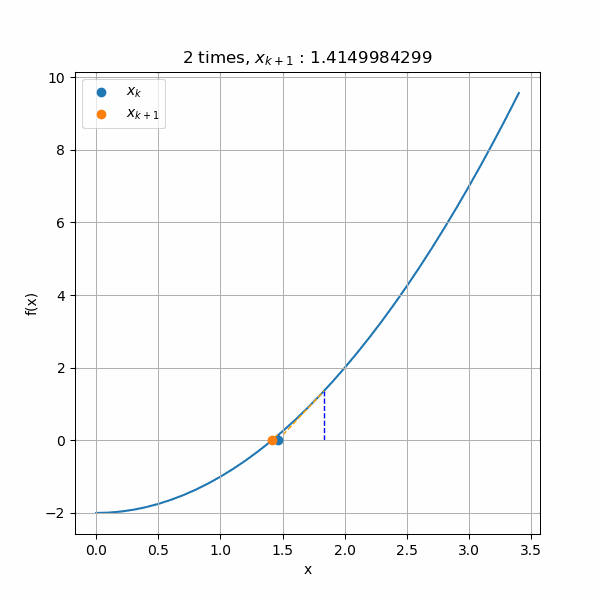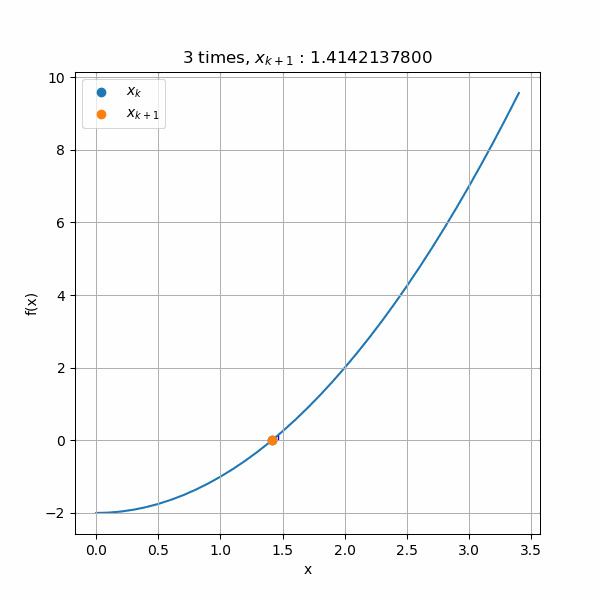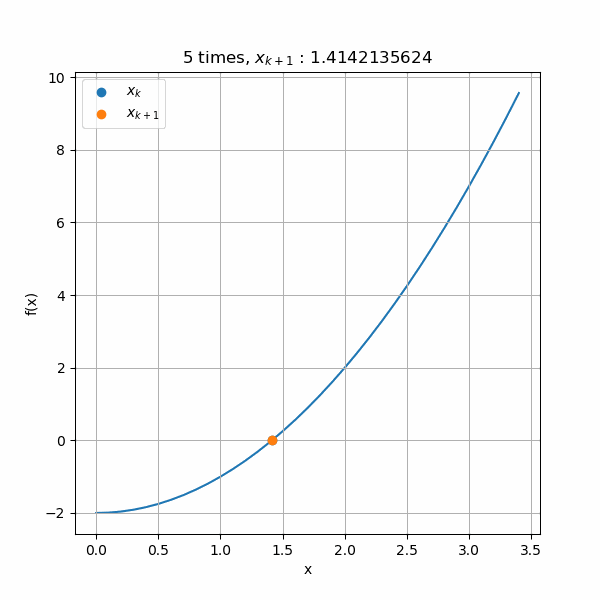



平方根を数値計算で求める ニュートン法 仕事と投資とあと何か



Q Tbn And9gcqus4h4vc2y4qfw2km3qq5fmbt4olxpu7fggyuxrbzpc6v0im5l Usqp Cau



2



Excel Vbaでニュートン法を計算してみる Excel Vbaによる数値解析 Excel 07編



ニュートン法による求根 Thoth Children




遂次近似法3 ニュートン法 演習 身勝手な主張
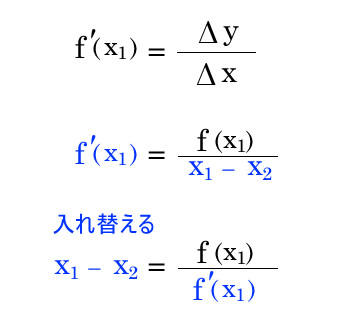



ニュートン法で近似解 Python Numpy 優技録



3



エクセルを用いたニュートン ラプソン法による非線形方程式の計算




高校数学 ニュートン法 F X 0の実数解と累乗根の近似値 受験の月
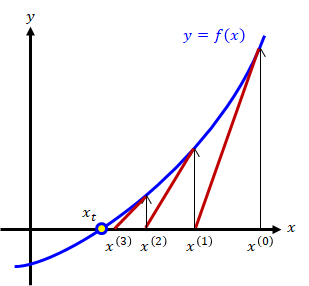



技術計算製作所 ニュートン法 機械設計に必要な情報とwebアプリ ソフトウエアを公開しています Science Numcal Newton




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト




数理最適化の勉強メモ 最急降下法 ニュートン法の原理と特徴 かみのメモ



R Source




Amazon Co Jp 確率微分方程式に対するnewton法 発見的なアルゴリズムの定式化から確率論的二次収束まで Ebook 天野一男 Kindleストア



Q Tbn And9gcqosnrs1e0zuuwlzv0rntb4bqur5dsqkixsdcu 4kdbjd5 Qpgl Usqp Cau



ニュートン法とは 制御工学の基礎あれこれ
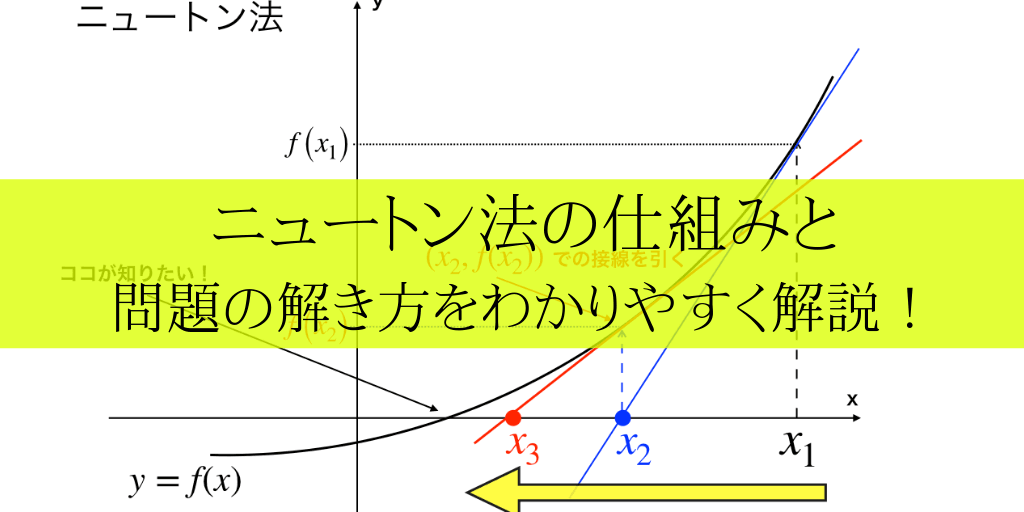



ニュートン法の仕組みと証明の仕方を分かりやすく解説
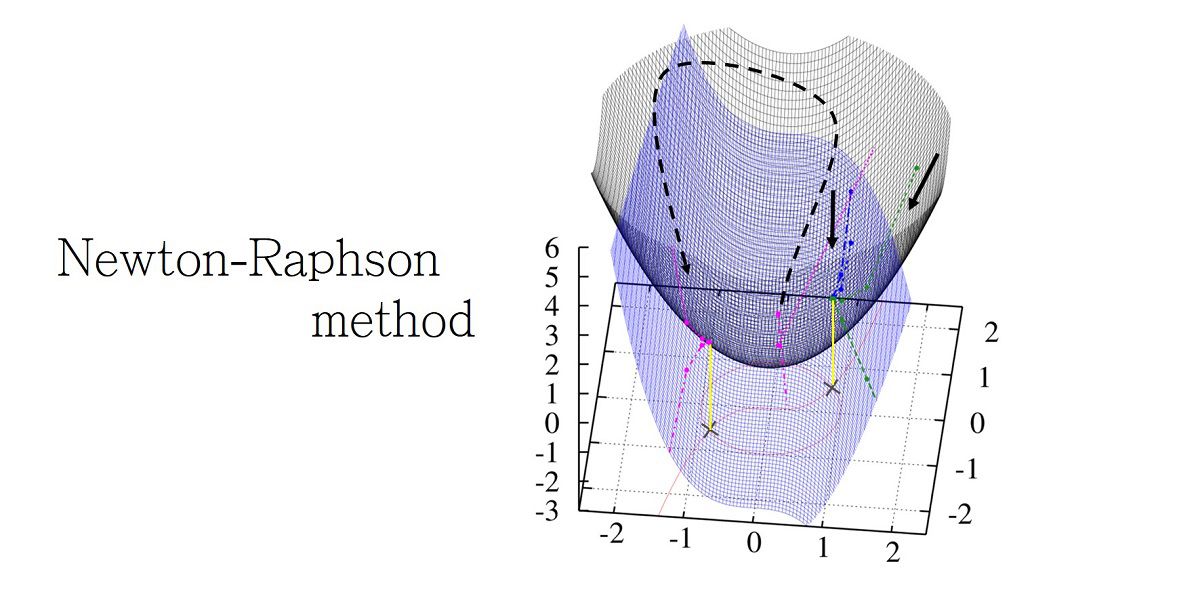



ニュートン法 1 2次元 多次元 シキノート




ニュートン法 Newton S Method Youtube
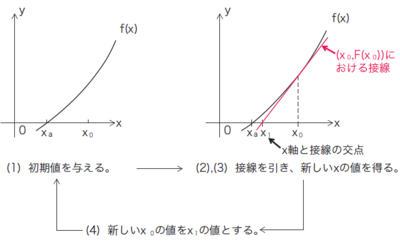



第67回 微分 積分の数学 ニュートン ラフソン法 前編 はじめmath Javaでコンピュータ数学 Gihyo Jp 技術評論社




ニュートン法の例題 ルート3の近似値を与える方法 理数アラカルト



楕円軌道とケプラー方程式 Kepler Equation




C 非線形方程式の解法 ニュートン法 Mk Mode Blog



Excel Vbaでニュートン法を計算してみる Excel Vbaによる数値解析 Excel 07編




11 号 電力システムの安定平衡点算出装置 Astamuse
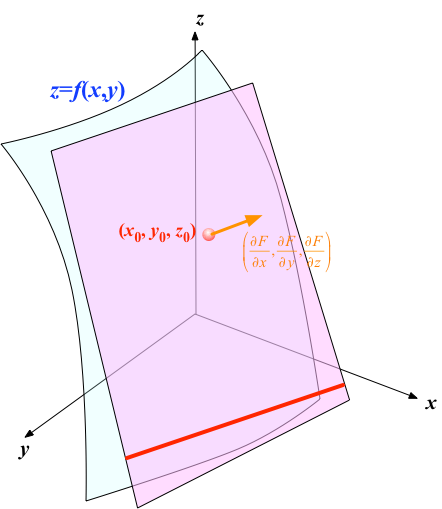



情報基礎 Pythonプログラミング ステップ7 多変数のニュートン法




微分積分6テイラー展開 ボンフェロニ補正 積率母関数 ニュートン法 Ryamada 数学 Kindleストア Amazon




C言語で非線形方程式の解法 ニュートン法 Pypy Com




Tech Tips 最急降下法とニュートン法の比較


